Stat-Ease Blog

Categories
Why it pays to be skeptical of three-factor-interaction effects
Quite often, when providing statistical help for Stat-Ease software users, our consulting team sees an over-selection of effects from two-level factorial experiments. Generally, the line gets crossed when picking three-factor interactions (3FI), as I documented in the lead article for the June 2007 Stat-Teaser. In this case, the experimenter picked all the estimable effects when only one main effect (factor B) really stood out on the Pareto plot. Check it out!
In my experience, the true 3FIs emerge only when one of the variables is categorical with a very strong contrast. For example, early in my career as an R&D chemical engineer with General Mills, I developed a continuous process for hydrogenating a vegetable oil. By cranking up the pressure and temperature and using an expensive, noble-metal catalyst (palladium on a fixed bed of carbon), this new approach increased the throughput tremendously over the old batch process, which deployed powered nickel to facilitate the reaction. When setting up my factorial experiment, our engineering team knew better than to make the type of reactor one of the inputs, because being so different, this would generate many complications of time-temperature interactions differing from on process to the other. In cases like this, you are far better off doing separate optimizations and then seeing which process wins out in the end. (Unfortunately for me, I lost this battle due to the color bodies in the oil poisoning my costly catalyst.)
A response must really behave radically to require a 3FI for modeling as illustrated hypothetically in Figures 1 versus 2 for two factors—catalyst level (B) and temperature (D)—as a function of a third variable (E)—the atmosphere in the reactor.

Figures 1 & 2: 3FI (BDE) surface with atmosphere of nitrogen vs air (Factor E at low & high levels)
These surfaces ‘flip-flop’ completely like a bird in flight. Although factor E being categorical does lead to a strong possibility of complex behavior from this experiment, the dramatic shift caused by it changing from one level to the other would be highly unusual by my reckoning.
It turns out that there is a middle ground with factorial models that obviates the need for third-order terms: Multiple two-factor interactions (2FIs) that share common factors. The actual predictive model, derived from a case study we present in our Modern DOE for Process Optimization workshop, is:
Yield = 63.38 + 9.88*B + 5.25*D − 3.00*E + 6.75*BD − 5.38*DE
Notice that this equation features two 2FIs, BD and DE, that share a common factor (D). This causes the dynamic behavior shown in Figures 3 and 4 without the need for 3FI terms.

Figure 3 & 4: 2FI surface (BD) for atmosphere of nitrogen vs air (Factor E at low & high levels)
This simpler model sufficed to see that it would be best to blanket the batch reactor with nitrogen, that is, do not leave the hatch open to the air—a happy ending.
Conclusion
If it seems from graphical or other methods of effect selection that 3FI(s) should be included in your factorial model, be on guard for:
- Over-selection of effects (my first case)
- The need for a transformation (such as log): Be sure to check the Box-Cox plot (always!).
- Outlier(s) in your response (look over the diagnostic plots, especially the residual versus run).
- A combination of these and other issues—ask stathelp@statease.com for guidance if you use Stat-Ease software (send in the file, please).
I never say “never”, so if you really do find a 3FI, get back to me directly.
-Mark (mark@statease.com)
2021 Online DOE Summit

Stat-Ease is hosting an amazing group of speakers for the 2021 Online DOE Summit. Taking place on September 28 & 29, this conference will be accessible to technical professionals around the globe. Register to attend the live in-person sessions via GotoWebinar, or plan to watch the on-demand recordings after the conference. Registration is free of charge.
Here is the line-up:
Speakers - September 28:
(Time 10am - 2pm US Central Time)
Hour 1: (Keynote) Martin Bezener (President & Chief Technical Officer, Stat-Ease)
Stat-Ease 360 Reveal

Hour 2: Gregory Hutto (Wing Operations Analyst, US Air Force)
The Tooth Fairy in Experimental Design: White Lies We Tell Our Software
Hour 3: Drew Landman (Professor & Associate Chair, Dept of Mech & Aero Engr, Old Dominion University)
An I-Optimal Split-Plot Design for eVTOL Tilt-Rotor Performance Characterization
Hour 4: Jason Pandolfo (Research Scientist, Quaker Chemical)
Using Logistic Regression to Predict the Stability of Metalworking Fluid Emulsions in Varying Water Quality Conditions
Speakers - September 29:
(Time 10am - 2pm US Central Time)
Hour 1: (Keynote) Hank Anderson (VP Software Development, Stat-Ease)
Python Integration with Stat-Ease 360 - A Tutorial

Hour 2: Oliver Thunich (Statistics Consultant, STATCON GmbH)
Adjusting a DOE to Unpredictable Circumstances
Hour 3: Steven Mullen (Senior Scientist, Cook Medical)
Improving Process Understanding of an IVF Cell Culture Incubator via Response Surface Methodology
Hour 4: Gregory Perrine (Research Scientist, Georgia-Pacific)
Debonder Formulation Optimization Using a KCV Mixture/Process Design in Paper Handsheets
We look forward to seeing you!
Please send any questions to Shari@statease.com.
Avoiding Over-Selection of Effects on the Half-Normal Plot
One of the greatest tools developed by Cuthbert Daniel (1976), was the use of the half-normal plot to visually select effects for two-level factorials. Since these designs generally contain no replicates, there is no pure error to use as the base for statistical F-tests. The half-normal plot allows us to visually distinguish between the effects that are small (and normally distributed) versus large (and likely to be statistically significant). The subsequent ANOVA is built on this decision to split the effects into the few that are likely “signal” versus the majority that are likely “noise”.
Often the split between the groups is obvious, with a clear gap between them (see Figure 1), but sometimes it is more ambiguous and harder to decide where to “draw the line” (see Figure 2).
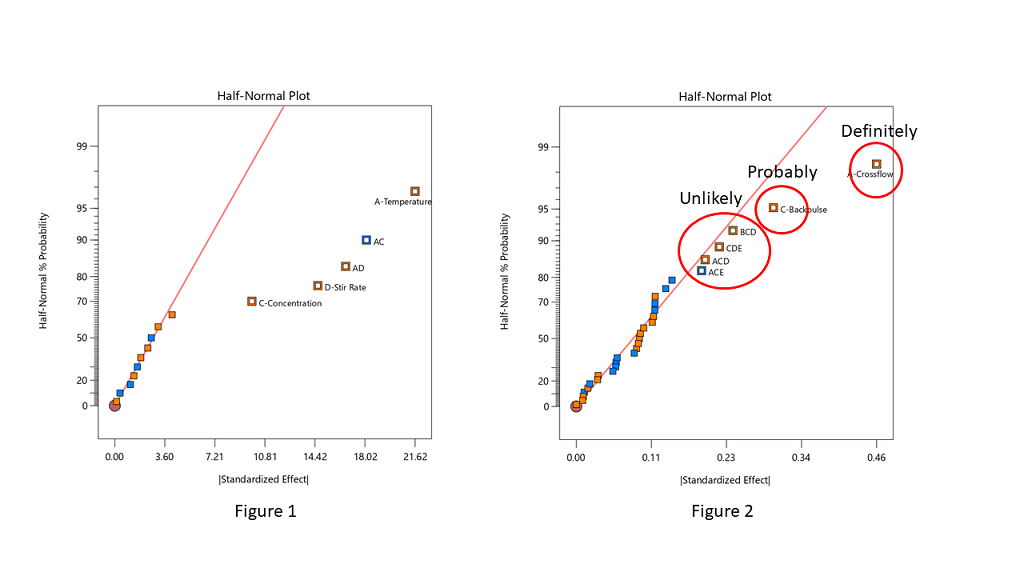
Stat-Ease consultants recommend staying conservative when deciding which effects to designate as the “signal”, and to be cautious about over-selecting effects. In Figure 2, the A effect is clearly different from the other effects and should definitely be selected. The C effect is also separated from the other effects by a “gap” and is probably different, so it should also be included in the potential model terms. The next grouping consists of four three-factor interactions (3FI’s.) Extreme caution should be exercised here – 3FI terms are very rare in most production and research settings. Also, they fall “on the line”, which indicates that they are most likely within the normal probability curve that contains the insignificant effects. These terms should be pooled together to estimate the error of the system. The conservative approach says that choosing A and C for the model is best. Adding any other terms is most likely just chasing noise.
Hints for choosing effects:
- Split the effects into two groups, distinguishing between the “big” and “small” ones, right versus left, respectively
- Start from the right side of the graph – that is where the biggest effects are
- Look for gaps that separate big effects from the rest of the group
- STOP if you select a 3FI term – these are very unlikely to be real effects (throw them back into the error pool)
- Don’t skip a term – if a smaller effect looks like it could be significant, then all larger effects also must be included
- Effects need to “jump off” the line – otherwise they are just part of the normal distribution
Sometimes you have to simply accept that the changes in the factor levels did not trigger a change in the response that was larger than the normal process variation (Figure 3). Note in Figure 3 that the far right points are straddling the straight line. These terms have virtually the same size effect – don’t select the lower one just because it is below the line.

When you are lucky enough to have replicates, the pure error is then used to help position green triangles on the half-normal plot. The triangles span the amount of error in the system. If they go out farther than the biggest effect, that is a clear indication that there are no effects that are larger than the normal process variation. No effects are significant in this case (see Figure 4).
Conclusion
The half-normal plot of effects gives us a visual tool to split our effects into two groups. However, the use of the tool is a bit of an art, rather than an exact science. Combine this visual tool with both the ANOVA p-values and, most importantly, your own subject matter knowledge, to determine which effects you want to put into the final prediction model.
Cutting-Edge Tools in Design-Expert Version 13
Version 13 of Design-Expert® software (DX13) provides a substantial step up on ease of use and statistical power for design of experiments (DOE). As detailed below, it lays out an array of valuable upgrades for experimenters and industrial statisticians. See DX13’s amazing features for yourself via our free, fully functional, trial download at www.statease.com/trial/.
Modify Design Space Wizard
Quite often an experiment leads to promising results that lie just beyond its boundaries. DX13 paves the way via its new wizard for modifying your design space. Press the Augment Design button, select “Modify design space” and off you go. Run through the “Modify Design Space – Reactive Extrusion” tutorial, available via program Help, to see how wonderfully this new wizard works. As diagrammed on its initial screen, the modify-design-space tool facilitates shrinking and moving your space, not just expanding it. And it works on mixture as well as process space.
Poisson regression
For assessing measures that come by counts, Poisson regression models fit with greater precision than ordinary methods. Demonstrate this via the “Poisson Regression – Antiseptic” tutorial where Poisson regression proves to be just the right tool for modeling colony forming units (CFU) in a cell culture. This new modeling tool, along with logistic regression for binary responses (introduced in version 12), puts Design-Expert at a very high level for a DOE-dedicated program.
Multiple analyses per individual response
Easily model any response in various ways to readily compare them. Then chose the model most fitting for achieving optimization goals. Simply press the plus [+] button on the Analysis branch. The Antiseptic tutorial demonstrates the utility of trying several modeling alternatives, none of which can do better than Poisson regression (but worth a try!).
Rounding factor or component settings
Optimal (custom) designs work wonderfully well for laying out statistically ideal experiments. However, the numerical levels they produce often extend to an inconvenient number of decimal places. No worries: DX13 provides a new “Round Columns” button—very convenient for central composite and optimal designs. As demonstrated in the Antiseptic tutorial, this works especially well for mixture components—maintaining their proper total while making the recipe far easier for the experimenter to accomplish. Do so either on the basis of significant digits (as shown) or by decimal places.
Import Data
DX13 makes it far easier to bring in existing data. Simply paste in your data from a spreadsheet (or another statistical program) and identify each column as an input or output. If you paste in headers, right click rows to identify names and units of measure. For example, DX13 enables entry of the well-known Longley data (see the “Historical Data – Unemployment” tutorial for background) directly from an Excel spreadsheet. Easy! Once in Design-Expert, its advanced tools for design evaluation, modeling and graphics can be put to good use.
More Enhancements
Design
- The Constraints node now allows you to modify existing limits: Second thoughts? No problem!
- New ribbon with easy access to versatile design-layout features such as Change View, and Hide/Show Columns
- Runs outside the constraints flagged, but still usable for analysis; furthermore, they can be moved back into the valid space via the right-click menu
- Adding verification runs after an analysis no longer invalidates it
- Continuous and discrete numeric factors now indicated in the Design Summary
Analysis
- Response name now included when copying equations to Excel
- Pearson, Deviance, and Hosmer-Lemeshow goodness-of-it tests added for logistic regression
Diagnostics
- New preference for the default layout of the Diagnostics tabs
Graphs
- Box (and whiskers) Plot for Graph Columns: Another very useful tool for data exploration prior to analysis.
- Control multiple graphs at the same time with the factors tool: Side-by-side interactive views—enlightening!
- Perturbation and trace plots now colored by factor
- New All-Factor graphs option shows only factors selected for the model
- When the number of tick-marks becomes large, only a subset is shown
- For large designs, the Leverage graph scales to maximum value, rather than 1
- When FDS-graph crosshair goes above 80% it changes to black, rather than red
Christmas Trees on my Effects Plot?
As a Stat-Ease statistical consultant, I am often asked, “What are the green triangles (Christmas trees) on my half-normal plot of effects?”
Factorial design analysis utilizes a half-normal probability plot to identify the largest effects to model, leaving the remaining small effects to provide an error estimate. Green triangles appear when you have included replicates in the design, often at the center point. Unlike the orange and blue squares, which are factor effect estimates, the green triangles are noise effect estimates, or “pure error”. The green triangles represent the amount of variation in the replicates, with the number of triangles corresponding to the degrees of freedom (df) from the replicates. For example, five center points would have four df, hence four triangles appear. The triangles are positioned within the factor effects to reflect the relative size of the noise effect. Ideally, the green triangles will land in the lower left corner, near zero. (See Figure 1). In this position, they are combined with the smallest (insignificant) effects and help position the red line. Factor effects that jump off that line to the right are most likely significant. Consider the triangles as an extra piece of information that increases your ability to find significant effects.

Once in a while we encounter an effects plot that looks like Figure 2. “What does it mean when the green triangles are out of place - on the upper right side instead of the lower left?”
This indicates that the variation between the replicates is greater than the largest factor effects! Since this error is part of the normal process variation, you cannot say that any of the factor effects are statistically significant. At this point you should first check the replicate data to make sure it was both measured and recorded correctly. Then, carefully consider the sources of process variation to determine how the variation could be reduced. For a situation like this, either reduce the noise or increase the factor ranges. This generates larger signals that allow you to discover the significant effects.

- Shari Kraber
For statistical details, read “Use of Replication in Almost Unreplicated Factorials” by Larntz and Whitcomb.
For more frequently asked questions, sign up for Mark’s bi-monthly e-mail, The DOE FAQ Alert.
