Stat-Ease Blog

Categories
The Design and Analysis of Launching Cats
Hi folks! It was wonderful to meet with so many new prospects and long-standing clients at the Advanced Manufacturing Minneapolis expo last week. One highlight of the show was running our own design of experiments (DOE) in-booth: a test to pinpoint the height and distance of a foam cat launched from our Cat-A-Pult toy. Visitors got to choose a cat and launch it based on our randomized run sheet. We got lots of takers coming in to watch the cats fly, and we even got a visit from local mascot Goldy Gopher!

Mark, Tony, and Rachel are all UMN alums - go Gophers!
But I’m getting a bit ahead of myself: this experiment primarily shows off the ease of use and powerful analytical capabilities of Design-Expert® and Stat-Ease® 360 software. I’m no statistician – the last math class I took was in high school, over a decade ago – but even a marketer like me was able to design, run, and analyze a DOE with just a little advice. Here’s how it worked.
Let’s start at the beginning, with the design. My first task was to decide what factors I wanted to test. There were lots of options! The two most obvious were the built-in experimental parts of the toy: the green and orange knobs on either side of the Cat-A-Pult, with spring tension settings from 1 to 5.

However, there were plenty of other places where there could be variation in my ‘pulting system:
- The toy comes with 5 Cat-A-Pults: are there variations between each 'pult?
- Does it matter what kind of surface the Cat-A-Pult is on, e.g., wood, concrete, or carpet?
- The toy came with 5 colors of foam cat; would the pigment change the cat’s weight enough to matter?
- What about where on the plate we apply launch pressure, or how much pressure is applied?
Some of these questions can be answered with subject matter knowledge – in the case of launch pressure, by reading the instruction manual.

For our experiment, the surface question was moot: we had no way to test it, as the convention floor was covered in carpet. We also had no way to test beforehand if there were differences in mass between colors of cat, since we lacked a tool with sufficient precision. I settled on just testing the experimental knobs, but decided to account for some of this variation in other ways. We divided the experiment into blocks based on which specific Cat-A-Pult we were using, and numbered them from 1 to 5. And, while I decided to let people choose their cat color to enhance the fun aspect, we still tracked which color of cat was launched for each run - just in case.
Since my chosen two categoric factors had five levels each, I decided to use the Multilevel Categoric design tool to set up my DOE. One thing I learned from Mark is that these are an “ordinal” type of categoric factor: there is an order to the levels, as opposed to a factor like the color of the cat or the type of flooring (a “nominal” factor). We decided to just test 3 of the 5 Cat-A-Pults, trying to be reasonable about how many folks would want to play with the cats, so we set the design to have 3 replicates separated out into 3 blocks. This would help us identify if there were any differences between the specific Cat-A-Pults.

For my responses, I chose the Cat-A-Pult’s recommended ones: height and distance. My Stat-Ease software then gave me the full, 5x5, 25-run factorial design for this, with a total of 75 runs for the 3 replicates blocked by 'pult, meaning we would test every combination of green knob level and orange knob level on each Cat-A-Pult. More runs means more accurate and precise modeling of our system, and we expected to be able to get 75 folks to stop by and launch a cat.
And so, armed with my run sheet, I set up our booth experiment! I brought two measuring tapes for the launch zone: one laid along the side of it to measure distance, and one hanging from the booth wall to measure height. My measurement process was, shall we say, less than precise: for distance, the tester and I eyeballed the point at which the cat first landed after launch, then drew a line over to our measuring tape. For height, I took a video of the launch, then scrolled back to the frame at the apex of the cat’s arc and once again eyeballed the height measurement next to it. In addition to blocking the specific Cat-A-Pult used, we tracked which color of cat was selected in case that became relevant. (We also had to append A and B to the orange cat after the first orange cat was mistaken for swag!)

Whee! I'm calling that one at 23 inches.
Over the course of the conference, we completed 50 runs, getting through the full range of settings for ‘pults 1 and 2. While that’s less than we had hoped, it’s still plenty for a good analysis. I ran the analysis for height, following the steps I learned in our Finding the Vital Settings via Factorial Analysis eLearning module.


The half-normal plot of effects and the ANOVA table for Height.
The green knob was the only significant effect on Height, but the relatively low Predicted R² model-fit-statistic value of 0.36 tells us that there’s a lot of noise that the model doesn’t explain. Mark directed me to check the coefficients, where we discovered that there was a 5-inch variation in height between the two Cat-A-Pult! That’s a huge difference, considering that our Height response peaked at 27 inches.
With that caveat in mind, we looked at the diagnostic plots and the one-factor plot for Height. The diagnostics all looked fine, but the Least Significant Difference bars showed us something interesting: there didn’t seem to be significant differences between setting the green knob at 1-3, or between settings 4-5, but there was a difference between those two groups.

One-factor interaction plot for Height.
With this analysis under my belt, I moved on to Distance. This one was a bit trickier, because while both knobs were clearly significant to the model, I wasn’t sure whether or not to include the interaction. I decided to include it because that’s what multifactor DOE is for, as opposed to one-factor-at-a-time experimentation: we’re trying to look for interactions between factors. So once again, I turned to the diagnostics.

The three main diagnostic plots for Distance.
Here's where I ran into a complication: our primary diagnostic tools told me there was something off with our data. There’s a clear S-shaped pattern in the Normal Plot of Residuals and the Residuals vs. Predicted graph shows a slight megaphone shape. No transform was recommended according to the Box-Cox plot, but Mark suggested I try a square-root transform anyways to see if we could get more of the data to fit the model. So I did!

The diagnostics again, after transforming.
Unfortunately, that didn’t fix the issues I saw in the diagnostics. In fact, it revealed that there’s a chance two of our runs were outliers: runs #10 and #26. Mark and I reviewed the process notes for those runs and found that run #10 might have suffered from operator error: he was the one helping our experimenter at the booth while I ran off for lunch, and he reported that he didn’t think he accurately captured the results the way I’d been doing it. With that in mind, I decided to ignore that run when analyzing the data. This didn’t result in a change in the analysis for Height, but it made a large difference when analyzing Distance. The Box-Cox plot recommended a log transform for analyzing Distance, so I applied one. This tightened the p-value for the interaction down to 0.03 and brought the diagnostics more into line with what we expected.

The two-factor interaction plot for Distance.
While this interaction plot is a bit trickier to read than the one-factor plot for Height, we can still clearly see that there’s a significant difference between certain sets of setting combinations. It’s obvious that setting the orange knob to 1 keeps the distance significantly lower than other settings, regardless of the green knob’s setting. The orange knob’s setting also seems to matter more as the green knob’s setting increases.
Normally, this is when I’d move on to optimization, and figuring out which setting combinations will let me accurately hit a “sweet spot” every time. However, this is where I stopped. Given the huge amount of variation in height between the two Cat-A-Pults, I’m not confident that any height optimization I do will be accurate. If we’d gotten those last 25 runs with ‘pult #3, I might have had enough data to make a more educated decision; I could set a Cat-A-Pult on the floor and know for certain that the cat would clear the edge of the litterbox when launched! I’ll have to go back to the “lab” and collect more data the next time we’re out at a trade show.
One final note before I bring this story to a close: the instruction manual for the Cat-A-Pult actually tells us what the orange and green knobs are supposed to do. The orange knob controls the release point of the Cat-A-Pult, affecting the trajectory of the cat, and the green knob controls the spring tension, affecting the force with which the cat is launched.

I mentioned this to Mark, and it surprised us both! The intuitive assumption would be that the trajectory knob would primarily affect height, but the results showed that the orange knob’s settings didn’t significantly affect the height of the launch at all. “That,” Mark told me, “is why it’s good to run empirical studies and not assume anything!”
We hope to see you the next time we’re out and about. Our next planned conference is our 8th European DOE User Meeting in Amsterdam, the Netherlands on June 18-20, 2025. Learn more here, and happy experimenting!
Know the SCOR for a winning strategy of experiments
Observing process improvement teams at Imperial Chemical Industries in the late 1940s George Box, the prime mover for response surface methods (RSM), realized that as a practical matter, statistical plans for experimentation must be very flexible and allow for a series of iterations. Box and other industrial statisticians continued to hone the strategy of experimentation to the point where it became standard practice for stats-savvy industrial researchers.
Via their Management and Technology Center (sadly, now defunct), Du Pont then trained legions of engineers, scientists, and quality professionals on a “Strategy of Experimentation” called “SCO” for its sequence of screening, characterization and optimization. This now-proven SCO strategy of experimentation, illustrated in the flow chart below, begins with fractional two-level designs to screen for previous unknown factors. During this initial phase, experimenters seek to discover the vital few factors that create statistically significant effects of practical importance for the goal of process improvement.

The ideal DOE for screening resolves main effects free of any two-factor interactions (2FI’s) in broad and shallow two-level factorial design. I recommend the “resolution IV” choices color-coded yellow on our “Regular Two-Level” builder (shown below). To get a handy (pun intended) primer on resolution, watch at least the first part of this Institute of Quality and Reliability YouTube video on Fractional Factorial Designs, Confounding and Resolution Codes.
If you would like to screen more than 8 factors, choose one of our unique “Min-Run Screen” designs. However, I advise you accept the program default to add 2 runs and make the experiment less susceptible to botched runs.

Stat-Ease® 360 and Design-Expert® software conveniently color-code and label different designs.
After throwing the trivial many factors off to the side (preferably by holding them fixed or blocking them out), the experimental program enters the characterization phase (the “C”) where interactions become evident. This requires a higher-resolution of V or better (green Regular Two-Level or Min-Run Characterization), or possibly full (white) two-level factorial designs. Also, add center points at this stage so curvature can be detected.
If you encounter significant curvature (per the very informative test provided in our software), use our design tools to augment your factorial design into a central composite for response surface methods (RSM). You then enter the optimization phase (the “O”).
However, if curvature is of no concern, skip to ruggedness (the “R” that finalizes the “SCOR”) and, hopefully, confirm with a low resolution (red) two-level design or a Plackett-Burman design (found under “Miscellaneous” in the “Factorial” section). Ideally you then find that your improved process can withstand field conditions. If not, then you will need to go back up to the beginning for a do-over.
The SCOR strategy, with some modification due to the nature of mixture DOE, works equally well for developing product formulations as it does for process improvement. For background, see my October 2022 blog on Strategy of Experiments for Formulations: Try Screening First!
Stat-Ease provides all the tools and training needed to deploy the SCOR strategy of experiments. For more details, watch my January webinar on YouTube. Then to master it, attend our Modern DOE for Process Optimization workshop.
Know the SCOR for a winning strategy of experiments!
Dive into Diagnostics for DOE Model Discrepancies
Note: If you are interested in learning more, and to see these graphs in action, check out this YouTube video “Dive into Diagnostics to Discover Data Discrepancies”
The purpose of running a statistically designed experiment (DOE) is to take a strategically selected small sample of data from a larger system, and then extract a prediction equation that appropriately models the overall system. The statistical tool used to relate the independent factors to the dependent responses is analysis of variance (ANOVA). This article will lay out the key assumptions for ANOVA and how to verify them using graphical diagnostic plots.
The first assumption (and one that is often overlooked) is that the chosen model is correct. This means that the terms in the model explain the relationship between the factors and the response, and there are not too many terms (over-fitting), or too few terms (under-fitting). The adjusted R-squared and predicted R-squared values specify the amount of variation in the data that is explained by the model, and the amount of variation in predictions that is explained by the model, respectively. A lack of fit test (assuming replicates have been run) is used to assess model fit over the design space. These statistics are important but are outside the scope of this article.
The next assumptions are focused on the residuals—the difference between an actual observed value and its predicted value from the model. If the model is correct (first assumption), then the residuals should have no “signal” or information left in them. They should look like a sample of random variables and behave as such. If the assumptions are violated, then all conclusions that come from the ANOVA table, such as p-values, and calculations like R-squared values, are wrong. The assumptions for validity of the ANOVA are that the residuals:
- Are (nearly) independent,
- Have a mean = 0,
- Have a constant variance,
- Follow a well-behaved distribution (approximately normal).
Independence: since the residuals are generated based on a model (the difference between actual and predicted values) they are never completely independent. But if the DOE runs are performed in a randomized order, this reduces correlations from run to run, and independence can be nearly achieved. Restrictions on the randomization of the runs degrade the statistical validity of the ANOVA. Use a “residuals versus run order” plot to assess independence.
Mean of zero: due to the method of calculating the residuals for the ANOVA in DOE, this is given mathematically and does not have to be proven.
Constant variance: the response values will range from smaller to larger. As the response values increase, the residuals should continue to exhibit the same variance. If the variation in the residuals increases as the response increases, then this is non-constant variance. It means that you are not able to predict larger response values as precisely as smaller response values. Use a “residuals versus predicted value” graph to check for non-constant variance or other patterns.
Well-behaved (nearly normal) distribution: the residuals should be approximately normally distributed, which you can check on a normal probability plot.
A frequent misconception by researchers is to believe that the raw response data needs to be normally distributed to use ANOVA. This is wrong. The normality assumption is on the residuals, not the raw data. A response transformation such as a log may be used on non-normal data to help the residuals meet the ANOVA assumptions.
Repeating a statement from above, if the assumptions are violated, then all conclusions that come from the ANOVA table, such as p-values, and calculations like R-squared values, are wrong, at least to some degree. Small deviations from the desired assumptions are likely to have small effects on the final predictions of the model, while large ones may have very detrimental effects. Every DOE needs to be verified with confirmation runs on the actual process to demonstrate that the results are reproducible.
Good luck with your experimentation!
Wrap-Up: Thanks for a great 2022 Online DOE Summit!
Thank you to our presenters and all the attendees who showed up to our 2022 Online DOE Summit! We're proud to host this annual, premier DOE conference to help connect practitioners of design of experiments and spread best practices & tips throughout the global research community. Nearly 300 scientists from around the world were able to make it to the live sessions, and many more will be able to view the recordings on the Stat-Ease YouTube channel in the coming months.
Due to a scheduling conflict, we had to move Martin Bezener's talk on "The Latest and Greatest in Design-Expert and Stat-Ease 360." This presentation will provide a briefing on the major innovations now available with our advanced software product, Stat-Ease 360, and a bit of what's in store for the future. Attend the whole talk to be entered into a drawing for a free copy of the book DOE Simplified: Practical Tools for Effective Experimentation, 3rd Edition. New date and time: Wednesday, October 12, 2022 at 10 am US Central time.
Even if you registered for the Summit already, you'll need to register for the new time on October 12. Click this link to head to the registration page. If you are not able to attend the live session, go to the Stat-Ease YouTube channel for the recording.

Want to be notified about our upcoming live webinars throughout the year, or about other educational opportunities? Think you'll be ready to speak on your own DOE experiences next year? Sign up for our mailing list! We send emails every month to let you know what's happening at Stat-Ease. If you just want the highlights, sign up for the DOE FAQ Alert to receive a newsletter from Engineering Consultant Mark Anderson every other month.
Thank you again for helping to make the 2022 Online DOE Summit a huge success, and we'll see you again in 2023!
Understanding Lack of Fit: When to Worry
An analysis of variance (ANOVA) is often accompanied by a model-validation statistic called a lack of fit (LOF) test. A statistically significant LOF test often worries experimenters because it indicates that the model does not fit the data well. This article will provide experimenters a better understanding of this statistic and what could cause it to be significant.
The LOF formula is:

where MS = Mean Square. The numerator (“Lack of fit”) in this equation is the variation between the actual measurements and the values predicted by the model. The denominator (“Pure Error”) is the variation among any replicates. The variation between the replicates should be an estimate of the normal process variation of the system. Significant lack of fit means that the variation of the design points about their predicted values is much larger than the variation of the replicates about their mean values. Either the model doesn't predict well, or the runs replicate so well that their variance is small, or some combination of the two.
Case 1: The model doesn’t predict well
On the left side of Figure 1, a linear model is fit to the given set of points. Since the variation between the actual data and the fitted model is very large, this is likely going to result in a significant LOF test. The linear model is not a good fit to this set of data. On the right side, a quadratic model is now fit to the points and is likely to result in a non-significant LOF test. One potential solution to a significant lack of fit test is to fit a higher-order model.

Case 2: The replicates have unusually low variability
Figure 2 (left) is an illustration of a data set that had a statistically significant factorial model, including some center points with variation that is similar to the variation between other design points and their predictions. Figure 2 (right) is the same data set with the center points having extremely small variation. They are so close together that they overlap. Although the predicted factorial model fits the model points well (providing the significant model fit), the differences between the actual data points are substantially greater than the differences between the center points. This is what triggers the significant LOF statistic. The center points are fitting better than the model points. Does this significant LOF require us to declare the model unusable? That remains to be seen as discussed below.
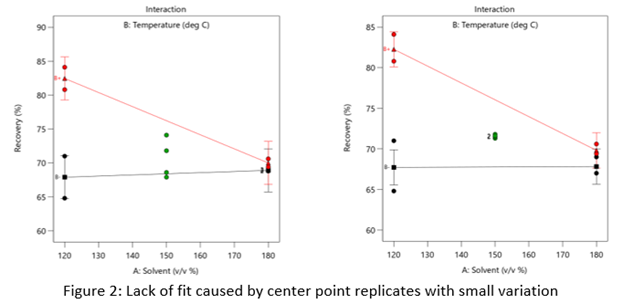
When there is significant lack of fit, check how the replicates were run— were they independent process conditions run from scratch, or were they simply replicated measurements on a single setup of that condition? Replicates that come from independent setups of the process are likely to contain more of the natural process variation. Look at the response measurements from the replicates and ask yourself if this amount of variation is similar to what you would normally expect from the process. If the “replicates" were run more like repeated measurements, it is likely that the pure error has been underestimated (making the LOF denominator artificially small). In this case, the lack of fit statistic is no longer a valid test and decisions about using the model will have to be made based on other statistical criteria.
If the replicates have been run correctly, then the significant LOF indicates that perhaps the model is not fitting all the design points well. Consider transformations (check the Box Cox diagnostic plot). Check for outliers. It may be that a higher-order model would fit the data better. In that case, the design probably needs to be augmented with more runs to estimate the additional terms.
If nothing can be done to improve the fit of the model, it may be necessary to use the model as is and then rely on confirmation runs to validate the experimental results. In this case, be alert to the possibility that the model may not be a very good predictor of the process in specific areas of the design space.
